To determine the value of acceleration due to gravity using angular oscillations of a long bar.
The purpose of this experiment is to use angular oscillations of rigid body in the form of a long bar for determining the acceleration due to gravity. The particular form of the body is chosen for the sake of simplicity in performing the experiment. The bar is hung from a knife-edge through one of the many holes along the length. It is free to oscillate about the knife-edge as axis. Any displacement θ, from the vertical position of equilibrium would give rise to an oscillatory motion just as in the case of a simple pendulum. The difference is that since this is rotating rigid body here we consider the torque of the gravitational force giving rise to the angular acceleration.
The restoring torque τ for an angular displacement θ is
(2.1)τ = −Mgd sinθ
where M is the mass of the compound pendulum and d the distance between the point of suspension O and the centre of mass of the bar C.
Since τ is proportional to sin θ, rather than θ, the condition for simple angular harmonic motion does not, in general, hold here. For small angular displacements, however, the relation sin θ ≈ θ is a good approximation, so that for small amplitudes in turn for small values of θ.
(2.2)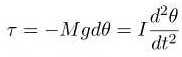
where I is the moment of inertia of the bar about the point of suspension O. The solution of the above equation is given by
(2.3) , (2.4)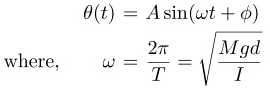
is the angular velocity of the compound pendulum. Thus, the period of oscillation is given by
(2.5)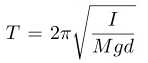
Due to the parallel axis theorem we have
(2.6)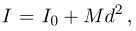
where, I 0 is the moment of inertia of the pendulum about it’s center of gravity (C.G). Inserting Eq. (2.6) in Eq. (2.5), we get the complete d dependence of the time period T as
(2.7)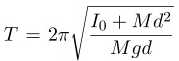
Since I 0 can be expressed as M k 2 , where k is the radius of gyration, Eq. (2.7) can be rewritten as
(2.8)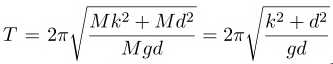
A simple pendulum consists of a mass m hanging at the end of a string of length L. The time period of a simple pendulum is given by
(2.9)
So, the time period of a simple pendulum equals the time period of a compound pendulum when
(2.10)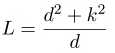
Re-arranging the above equation
(2.11)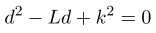
gives us a quadratic equation in d. If d1 and d2 are the two solutions of the above equation, then we find
(2.12)d1 + d2 = L
(2.13)d1.d2 = k
Since both d 1 and d 2 are positive, we conclude that there are two point of suspensions on one side of the C.G. of the compound pendulum where the time periods are equal. Similarly, there are two points of suspension on the other side of the C.G where the time periods are same. Thus, for a compound pendulum, there are four points of suspension, two on either side of the C.G. where the time periods are equal. The simple equivalent length L is sum of two of these point of suspension located asymmetrically on two sides of the C.G.
To facilitate further analysis it is useful to square Eq. (2.7) to get
(2.14)
In order to gain insight in the dependence of T on d let us first look at the dependence for (i) small d and (ii) large d. For small d (specifically for M.d^2 << I0 ) we have
(2.15) , (2.16)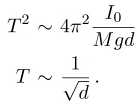
Thus T decreases as d increases. In the opposite limit i.e. for large d (specifically for M d 2 >> I 0 ) we have
(2.17) , (2.18)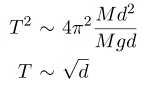
Thus T increases as d increases in this case. Physically the origins of d^2 in the numerator is coming from the expression for the moment of inertia I ∼ d^2 .
It is then just a question of which effect dominates for a given values of d. To under- stand this better (or more quantitatively) let us looks at the turning point. The minimum of the expression for T^2 as a function of d can be determined by taking the taking deriva- tive of T^2 with respect to d and setting it equal to zero (and ensuring the sign of the second derivative term corresponds to a minimum). Following this procedure gives
(2.19)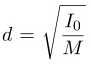
Eq. (2.19) can be written as I0 = M.d^2 . This relation is satisfied at the minimum or at the turning point. Using this in Eq. (2.7) we find that the turning point occurs when the magnitude of the two terms of the numerator are equal. For M.d^2 << I0 the I 0 term dominates in the numerator and d dependence is given by the denominator. In the region M.d^2 >> I0 the M.d^2 term dominates in the numerator and so the d dependence is dominated by the numerator.
Galileo was the first person to show that at any given place, all bodies fall freely when dropped, with the same (uniform) acceleration, if the resistance due to air is negligible. The gravitational attraction of a body towards the center of the earth results in the same acceleration for all bodies at a particular location, irrespective of their mass, shape or material, and this acceleration is called the acceleration due to gravity, g. The value of g varies from place to place, being greatest at the poles and the least at the equator. However, direct measurement of the acceleration due to gravity is very difficult. Therefore, the acceleration due to gravity is often determined by indirect methods, for example, using a simple pendulum or a compound pendulum. If we determine g using a simple pendulum, the result is not very accurate because an ideal simple pendulum cannot be realized under laboratory conditions. Hence, a compound pendulum is used to determine the acceleration due to gravity in the laboratory.