UG Physics Lab

Aim :

1. To understand the diffraction, diffraction grating and how diffraction grating works with the help of basic diffraction grating equations and experimental studies.

2. To measure the wavelength of the light source with the help of diffraction grating.

Theory :

Preliminary discussion:

Interference refers to the interaction of two or more wave trains of light having the same frequency and having a phase difference which remains constant with time (coherent sources), so that they may combine with the result that the energy is not distributed uniformly in space but is a maximum at certain points and a minimum (perhaps zero) at others.

(8.1)

Diffraction phenomenon is described as the apparent bending of waves around small obstacles and the spreading out of waves past small openings. Diffraction patterns are marked by a rapid decrease in intensity with increasing distance from the center of the pattern.

A diffraction grating is made by making many parallel scratches on the surface of a flat piece of transparent material. It is possible to put a large number of scratches per centimeter on the material, e.g., the grating to be used has 6000 lines/cm on it. The scratches are opaque but the areas between the scratches can transmit light. Thus, a diffraction grating becomes a multitude of parallel slit sources when light falls upon it.

Diffraction grating equation

When parallel bundle of rays falls on the grating, these rays and their associated wave fronts form an orthogonal set so the wave fronts are perpendicular to the rays and parallel to the grating (as shown in Fig. 11.1). According to Huygens’ Principle, every point on a wave front acts like a new source, each transparent slit becomes a new source so cylindrical wave fronts spread out from each. These wave fronts interfere either constructively or destructively depending on how the peaks and valleys of the waves are related.

Whenever the difference in path length between the light passing through different slits is an integral number of wavelengths of the incident light, the light from each of these slits will be in phase, and then it will form an image at the specified location. Mathematically, the relation is simple

(11.1)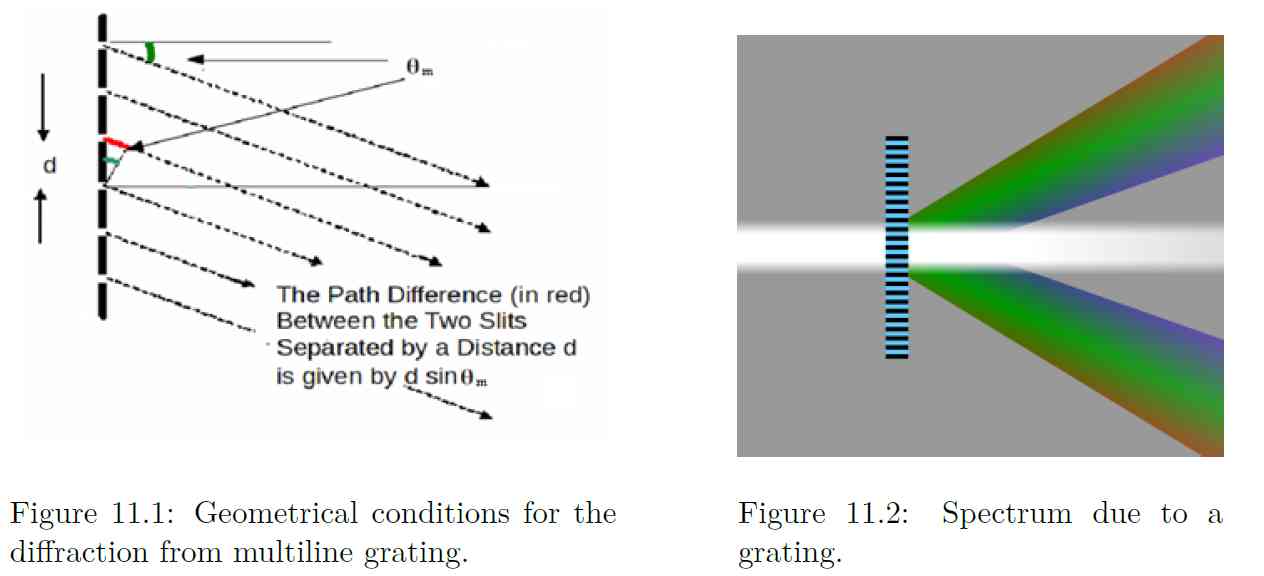

Eq. (11.1) is known as grating equation. The light that corresponds to direct transmission

(or specular reflection in the case of a reflection grating) is called the zero order, and is denoted m = 0. The other maxima occur at angles which are represented by non-zero integers m. Note that m can be positive or negative, resulting in diffracted orders on both side of the zero order beam.

Diffraction gratings are often used in monochromators, spectrometers, lasers, wavelength division multiplexing devices, optical pulse compressing devices, and many other optical instruments.

Resolving power of grating

This equation then leads to the following expression for the resolving power of the diffraction grating

(11.2)

R = λ/δλ = mN

Here λ is the average of wavelength, δλ is the difference between wavelengths, m is the order and N is the total number of slits on the grating. Thus, the distance between maxima depends on the distance between slits and the resolution,the relative sharpness of the maxima, depends on the total number of slits. (Often a grating is characterized by the number of slits per unit length. From this information one can, of course, deduce the distance between the slits..

Apparatus Required :

Spectrometer, diffraction grating, mercury light source, high voltage power supply, magnifying lens, spirit level, torch light, etc.

Procedure :

As with many optical instruments, the spectroscope requires some initial adjustments before the desired measurements can be performed. Focusing and levelling of the spectrometer for the parallel rays is to be done as per previous prism experiment.

Figure 11.3: Grating settings

To set the telescope axis perpendicular to that of the collimator:

Illuminate the slit with the light source. Turn the telescope of the spectrometer to view the image of the illuminated slit directly as shown in Fig. 11.3(a). The source should directly be in front of the slit such that maximum light falls on the slit. Adjust the cross-wires such that the image of the slit falls in the middle of the intersection of the cross-wires. Fix the prism table with the fixing screw and read any of the two verniers. Let this angle be α. Rotate the telescope by an amount 90 ± α such that it is exactly perpendicular to the collimator. Fix the telescope in this position and unfix the prism table.

Fix the grating (G) in the grating holder such that the grating lines are perpendicular to the prism table and the ruled surface extend equally on both sides of the center. The grating is set parallel to the line joining the prism table screws B and C as shown in Fig. 11.3. Turn the prism table such that light from the collimator is reflected into the telescope. The reflection should be by the unruled surface of the grating. To determine the unruled surface use the following procedure. Allow light to be reflected by both the grating surface one at a time and view the corresponding image via the telescope. The surface from which the image of the slit appears sharper is in fact the unruled surface of the grating

Once the unruled surface has been determined, view the reflection only via the unruled surface while the setup is as shown in Fig. 11.3(b). If the center of the grating displace either above or below the intersection of the cross-wires, then the grating surface is not vertical. To ensure that the grating surface is vertical, turn the prism table screws B and C equally in opposite directions until the center of the image coincides with the intersection of the cross-wires

Turn the unruled surface of the grating by an angle 45° such that the light from the collimator falls normally on the unruled surface of the grating. Fix the prism table in this position and unfix the telescope.

Even though we have made the plane of the grating vertical and the rulings perpendicular to the table surface, the rulings of the grating may not be vertical. In order to set the rulings vertical, rotate the telescope in its own plane on both side of the central image. On both sides on the central image different orders of image are seen as shown in Fig. 11.4. In the first order images on both sides, if the image on the left is higher than

Figure 11.4: Grating images of higher order

that of the image on the right or vice-versa, then turn the third screw A on the prism table until the images on both the sides are on the same level.

Caution

1. The diffraction grating is a photographic reproduction and should NOT be touched. Make sure that the glassy base of grating shouldn’t faces towards the source light.

2. Now your setup is ready to report the experimental observations.

Observations :

1. Check to make sure that the grating is not too high or low relative to the collimator. Affirm maximum brightness for the straight through beam by adjusting the source slit alignment. At this step, the slit should be narrow, perhaps a few times wider than the hairline. Search for the spectrum by moving the telescope to one side or the other. This spectrum should look much like the visible spectrum observed with the prism. This is the first order spectrum. Record for each color diffraction angle θR (along right side) and θL (along left side) from the straight trough beam.

2. For each of the seven colors in the mercury spectrum, measure the angles R and L to the nearest tenth of a degree by placing the hairline on the stationary side of the slit.

3. You are expected to observe the 1st order diffraction pattern.

4. From your observations calculate various wavelengths of visible radiations from the mercury source

Calculation

1. Use the grating equation with d = (1/6000) cm to find the wavelength for each colour.

2. Calculate % error for your reported λ measurement.

Table 11.1: For first order (m = 1). CSR - Circular scale reading, VSR - Vernier scale reading.

Result :

1. Percentage measurement error for your analysis.

2. A certain colour emerges at 15o in the first order spectrum. At what angle would this same colour emerge in the second order if the same source and grating are used?

3. What could be causing any discrepancy?

4. Why is it necessary that the base side of the grating face toward the light source? Draw a ray diagram for the two cases:

a) Base toward the source (correct).

b) Grating toward the source (incorrect).

5. Mention your special comments for each statement in your lab report as a part of experimental outputs.

Diffraction grating