UG Physics Lab

Aim :

1. To understand the accurate leveling and focusing of a spectrometer.

2. Investigation of the variation in the refractive index, μ of a prism with wavelength λ.

Theory :

The fact that a prism is capable of dispersing light is due to the variation of its refractive index with wavelength. In this experiment the refractive index is obtained for a variety of wavelengths by measuring the minimum deviation angle of the prism for each wavelength.

To understand what is meant by the term angle of minimum deviation, consider Fig. 5.1. The incident parallel light beam is refracted by the prism in such a way that it is deviated by the angle θd from the undeviated direction. The angle is known as the angle of deviation and varies with both the wavelength and the angle at which the incident light intersects the prism.

If the prism is rotated about the axis it is found that the angle of deviation changes but never becomes less than a certain minimum value, δmin known as the angle of minimum deviation i.e. no matter what the orientation of the prism, as long as it is in the path of the incident light beam, the light beam will be deviated through at least this angle. When the prism is oriented in such a way that the exit beam is deviated through the least possible angle δmin, then further rotation of the prism in either direction will cause the exit beam to move further away from the least deviated direction. Thus for each wavelength in a spectral light source, there is a variation of the angle of deviation, θd with the angle of incidence, θi and at some value of the angle of incidence, the angle of deviation reaches a minimum as seen in Fig. (5.3).

Relation between μ and λ

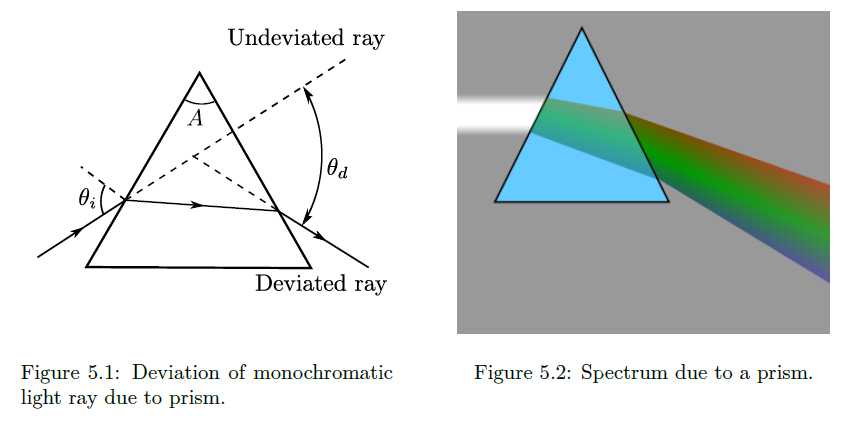
Figure 5.3: Variation of the angle of deviation (θd) with the angle of incidence (θi) for a particular wavelength.

by measuring δmin for a variety of wavelengths, the variation of μ with wavelength may be determined.

To derive the exact relationship, consider the prism as seen in Fig. (5.4). It can be shown that the minimum value of the angle of deviation, δmin occurs when the ray passes through the prism symmetrically i.e. when the angle at which the light emerges is equal to the angle of incidence such that the ray passes parallel to the base of the prism as in Fig. (5.4). At each face the ray changes direction by θi − θr and so the total minimum deviation is

(5.1)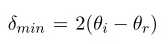

From Fig. 5.4, it is shown that the angle 6 MNO is the same as that of the refracting angle of the prism. Referring to the triangle LMN it is obvious, using trigonometry, that A = 2θr. Snell’s Law is of course μ = sin θi/ sin θr but θi = θmin/2 + θr, where θr = A/2 and hence we have

(5.2)

An empirical equation of the form

(5.3)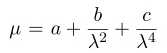

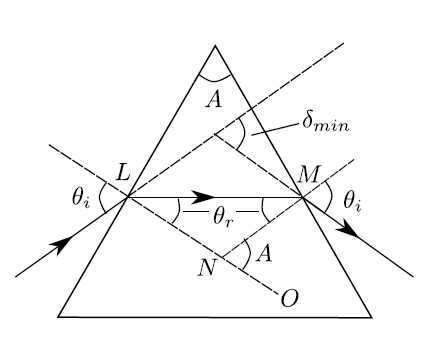
Figure 5.4: Condition for minimum deviation

was developed by Cauchy to describe the variation of μ with wavelength. Where a, b and c are constants and it is the purpose of this experiment to verify this equation (neglecting terms of higher order than the second) and to derive the constants a and b for the prism material.

Note: As the variation in refractive index over the whole of the visible is only of the order of 3% this means that δmin varies only very slowly with wavelength. Both a fair degree of experimental skill and great care in making the various measurements are necessary if reasonable results are to be attained.

Apparatus Required :

Spectrometer, prism, mercury light source, high voltage power supply, magnifying lens, spirit level, torch light etc.

Experimental procedure

Initially make sure you understand what each component of the spectrometer as detailed in Fig. (5.5) does. The experimental setup consists of following parts. To obtain satisfactory

Figure 4: Schematic diagram of the prism spectromete

results the spectroscope requires some initial adjustments before the desired measurements can be performed. For this experiment great care must be taken in adjusting the spectrometer so that the telescope is focused at infinity and the collimator set to give an accurately parallel beam. It is particularly important to ensure that the cross-hairs of the telescope are sharply visible and that no parallax exists between them and the spectral line images. The following steps should ensure this:

1. Focusing the telescope: Focus the telescope for the parallel rays from the distance object by sliding the eyepiece looking through telescope in and out, until a sharp image of object is seen. Due to the location of the laboratory this may not be possible so the building opposite may be used for this purpose.

2. Levelling the collimator: Place the spirit level on the collimator tube with its axis parallel to the axis of the tube. If the the bubble in the collimator is found to be displaced from its central position, turn the levelling screws provided with the collimator tube, in the same direction to bring the bubble back to its central position. This make the axis of the collimator tube horizontal.

3. Levelling of the prism table: There are three levelling screws A, B, C just below the prism table for levelling the table. There are parallel lines drawn on the prism table parallel to the line joining the screws B and C. Place the spirit level parallel to these lines and bring the bubble to the central position by turning the screws B and C equally in opposite directions. Now place the spirit level perpendicular to the line BC. If the bubble is not in the central position, then turn the A screw alone to bring the bubble in the center. Continue this for a couple of times until the bubble is in the center in both the positions. This makes the table vertical to the axis of rotation.

4. Focusing the collimator: Place a discharge lamp (Mercury lamp as a visible light source) in front of the spectroscope and turn the telescope until it is in line with and pointing directly at the collimator. Looking through the telescope and adjusting the position of the focusing screw on the collimeter until a sharp image of the slit is observed in the telescope. The collimeter now gives parallel rays which will fall on the prism.

Finding the least count for the spectrometer

It should be noted by the student that 30 vernier scale divisions (VSD) coincides with 29 circular scale divisions (CSD). So,

(5.4),(5.5)

Therefore, the least count

(5.6),(5.7)

Since 1 CSD = (1/2)° = 30', we have

(5.8)

Figure 5.6: Measurement of the reflecting angle of prism.

Measurement of the angle of prism (A)

1. Set up the prism and spectrometer as in Fig. (5.6). Lock the prism table.

2. Place the telescope cross-hairs in turn on the image of the slit reflected from surface AB and then surface AC.

3. At each position record the angular position of the telescope on the vernier scalethe angle between the two positions of the telescope is 2A, twice the apex angle of the prism and hence A can be found.

4. Repeat above step 2 and 3 to get an average value for A(~60°).

Viewing the spectrum due to refraction

The telescope and prism are rotated until the spectrum formed by refraction is found. The approximate prism position is shown in Fig. 5.7.

Further rotation of the prism while viewing the spectrum through the telescope will result in reaching the angle of minimum deviation. This is where the spectral lines “turn back" on themselves i.e. move opposite to their initial direction of travel while the prism is still being rotated in the same direction.

Position the prism and telescope so that the spectral lines are at the angle of minimum deviation i.e. at the point where the spectral lines “turn back" on themselves.

Turning the prism towards the telescope, increases the angle of incidence, thus moving to the right hand side of δmin in the curve of Fig. (5.3). Conversely turning the prism towards the collimator, decreases the angle of incidence, hence moving through the angle of minimum deviation to the left hand side of the curve of Fig. 5.3.

Measurement of the angle of minimum deviation, δmin for each wavelength

1. Using the Hg spectral lamp, observe the first order field of view of refracted spectrum. Find the point of minimum deviation for the Hg spectrum. The approximate prism position is as shown in Fig. 5.7.

Figure 5.7: Prism position for viewing the spectrum due to refraction

Table 5.1: Discharge lamp wavelengths

(Remember minimum deviation corresponds to the point at which movement of the lines of the Hg spectrum over the field of view of the telescope is reversed, although direction of rotation of the telescope continues in the same sense.)

2. Several spectral lines should be in the field of view of the telescope. Position the telescope on the highest wavelength spectral line and lock the prism table and telescope. It is essential that the prism and prism table remain in this position for the remainder of the experiment

3. Using the telescope fine adjustment screw, position the crosshairs of the telescope accurately on the spectral line of interest and read the vernier to the nearest minute of arc

4. The above step can be repeated for the other lines in the field of view of the telescope there should be enough movement in the telescope fine adjustment screw to allow positioning of the cross-hairs on all of the Hg spectral lines of Table 5.1 without unlocking the telescope again. If this is not the case, just unlock the telescope and reposition it such that the crosshairs of the eyepiece are on the spectral line of interest. It is imperative that the prism and prism table remain in their original fixed position.

5. Rotate the telescope anticlockwise until the undeviated image of the slit through the prism is in the field of view. Again position the crosshairs on the centre of the clit image and record the angular reading of the telescope on the vernier scale.

6. The actual value for δmin for each wavelength is the difference between the appropriate angular reading of the telescope position for minimum deviation and for the undeviated (straight through) position as seen in Fig. (5.1)

Observations :

Measurement of angle of prism (A)

Least count of the spectrometer (l.c.) = .......

Table 5.2: Table for measuring angle of prism (A). CSR - Circular scale reading, VSR -Vernier scale reading.

Measurement of angle of minimum deviation (δmin)

Angle by undeviated ray (θ') = ...... (CSR) + ...... (l.c) × ....... (VSR) = ..... (Total)

Calculations :

1. Calculate the refractive index μ, of the prism material for each wavelength using Eq. 5.2. Tabulate also a corresponding set of values for 1/λ^2.

2.Draw a graph of μ vs 1/λ^2.

3. Extract values for the Cauchy constants, a (intercept) and b (slope), of Eq. 5.3 from your graph. The least squares fitting routine can be used to get a more accurate value for a and b.

Result :

1. Calculate the refractive index for different values of wavelengths.

Table 5.3: Table for measuring angle of minimum deviation. CSR - Circular scale reading, VSR - Vernier scale reading.

Notes

Subtraction of angles (Mathematical)

Try to substract 45°25' from 90°15' . (Hint: Remember that 1° = 60').

Note about calculators

1. Some calculators are not able to handle degree and minutes. Make sure the degree minutes in these cases are converted to fractional degree via the conversion 1° = 60'.

2. Make sure your calculator is set to degree and not to radian or gradient.

Figure 5.8: Difference of angles in the two cases should be as follows: (a) δ = |θ2 − θ1| and (b) δ = (360 − θ1) + θ2 = 360 − (θ1 − θ2).

Refractive index of glass with the help of a prism